Alignment introduction
Mikhail Dozmorov
Virginia Commonwealth University
02-17-2021
The genomics workflow
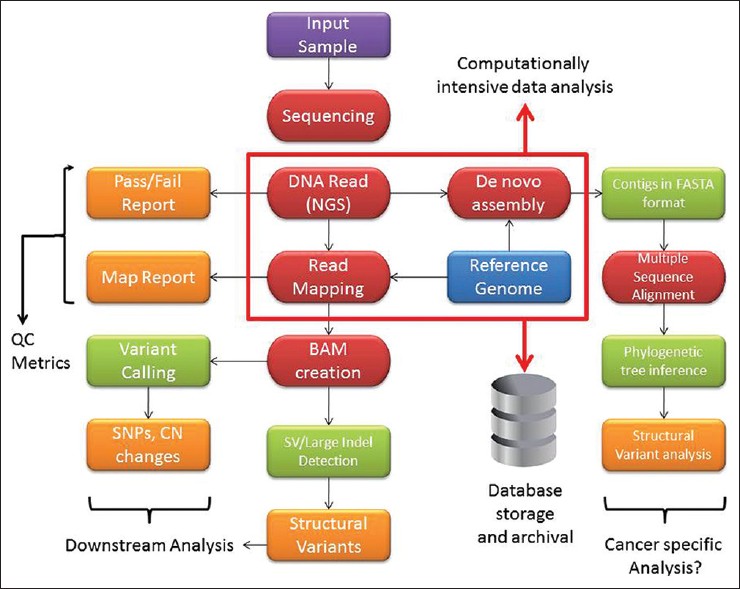
http://www.jpathinformatics.org/viewimage.asp?img=JPatholInform_2012_3_1_40_103013_u3.jpg
Alignment goals
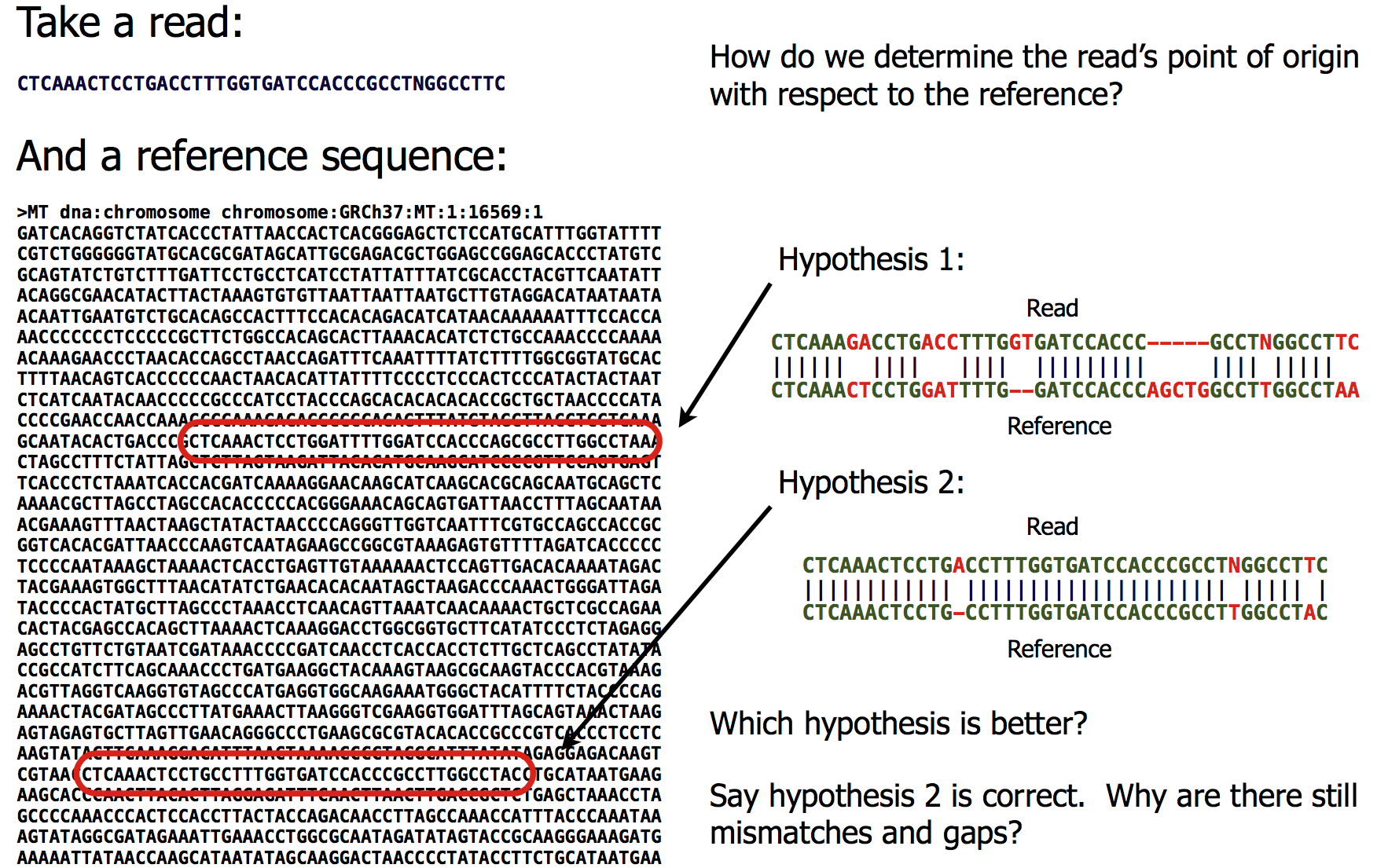
Alignment - the process by which we discover how or where the read sequence is similar to the reference sequence. Finding best match of the read sequence within the reference sequence.
- The human reference genome is big and complex (~3.2 billion bases)
- Sequencing data is big and complex (~1 billion short reads/run)
- Must find a home to each short read in the reference genome
Alignment goals
Poisson discribution
y5 <- dpois(x, 5); y10 <- dpois(x, 10); y15 <- dpois(x, 15)plot(x, y5, col = 1); lines(x, y10); lines(x, y15)
Estimating library complexity with a Poisson model
For Poisson sampling, we can write the (truncated) distribution over xi the times we sequence the ith molecule as: Pr(xi|λ)=1KL,R(λ)∗e−λλxixi! KL,R(λ)=R∑x=LPr(xi|λ) (The probability is 0 if xi is less than L or greater than R)
We can estimate the maximum likelihood rate parameter λ from a vector of observations x
Maximum likelihood library size
KL,R(λ)=R∑x=LPr(xi|λ)
- M unique sequences observed, maximum likelihood library size is
^C=MKL,R(λ)
- Approximate solution
^C=M1−Poisson(0,λ)
Problem with Poisson distribution
- Poisson Library Complexity model 150 '1000 Genome' Datasets
- Estimate library complexity from 10% of uniformly sampled reads vs. from all reads

- Poisson λ=Mean=Variance
- Gamma distributed sampling rates describe the entire population (library preparation)
\bigbreak
- Poisson sampling to form a smaller sample (sequencing)
\bigbreak
- Negative binomial distribution characterizes the resulting occurrence histogram

The gamma distribution is a "conjugate prior" for the Poission distribution
Poisson(x;λ)=λxe−λx!
Gamma(x,α,β)=βαxα−1e−βxΓ(α)
NB(y;α,β)=∫∞0Poisson(y;x)Gamma(x;α,β)dx
Negative Binomial model for sequence occurrences
- C - library complexity (latent, fit to observed data)
- N - number of reads
- M - total number of unique sequences
- λ=N/C
- k - dispersion (latent, fit to observed data)
Pr(xi,λ,k)=NB(xi|λ,k)=NB(xi|n,p)
- p=λ/(λ+1/k)
- n=1/k
Simulation results show that the Gamma Possion works well for non-uniform libraries
- True library complexity: 1M unique molecules
- Vary k (controls sampling rate variance)
- Given 100K reads ($\lambda=0.1$), assess estimates from both models
- k=0.1\ \ \ Poisson: 0.93M\ \ \ \ GP: 0.96M
- k=1\ \ \ \ \ Poisson: 0.52M\ \ \ \ GP: 1.01M
- k=10\ \ \ \ Poisson: 0.12M\ \ \ \ GP: 1.10M
- k=20\ \ \ \ Poisson: 0.07M\ \ \ \ GP: 0.68M
Negative Binomial Library Complexity better model 150 '1000 Genome' Datasets

- Data are "overdispersed" (variance greater than mean)
Marginal value of additional sequencing
- C – library complexity (latent – estimated)
- N – number of reads
- M – number of unique sequences
M can be estimated by (1−NegativeBinomial(0|λ,k))∗C
- Assume we have r more reads s=(N+r)/N
- Replace λ by s∗λ to estimate M′ achieved with r more reads
Marginal value of additional sequencing

End: MIT7_91JS14_Lecture5.pdf - BWT, FM index, https://www.youtube.com/watch?v=P3ORBMon8aw&list=PLUl4u3cNGP63uK-oWiLgO7LLJV6ZCWXac&index=5
-->
Genome Assembly Algorithms
Problem: Exact String Matching
Input: A text string T, where ∥T∥=n, and a pattern string P, where ∥P∥=m
Output: An index i such that Ti+j−1=Pj for all 1≤j≤m, i.e. showing that P is a substring of T
Analysis
This algorithm might use only n steps if we are lucky, e.g. T=aaaaaaaaaaa, and P=bbbbbbb
We might need ∼n×m steps if we are unlucky, e.g. T=aaaaaaaaaaa, and P=aaaaaab
We can’t say what happens "in practice", so we settle for a worst case scenario (longest possible running time)
Analysis
This algorithm might use only n steps if we are lucky, e.g. T=aaaaaaaaaaa, and P=bbbbbbb
We might need ∼n×m steps if we are unlucky, e.g. T=aaaaaaaaaaa, and P=aaaaaab
We can’t say what happens "in practice", so we settle for a worst case scenario (longest possible running time)
By being more clever, we can reduce the worst case to O(nm)
Certain generalizations won’t change this, like stopping after the first occurrence of the pattern
Certain other generalizations seem more complicated, like matching with gaps
Algorithm Complexity
We use the "Big oh" notation to state an upper bound on the number of steps that an algorithm takes in the worst case. Thus the brute force string matching algorithm is O(nm), or takes quadratic time
A linear time algorithm, i.e. O(n+m), is fast enough for almost any application
A quadratic time algorithm is usually fast enough for small problems, but not big ones, since 10002=1,000,000 steps is reasonable but 1,000,0002 is not
An exponential-time algorithm, i.e. O(2n) or O(n!), can only be fast enough for tiny problems, since 220 and 10! are already up to 1,000,000
Algorithm Complexity
Unfortunately, for many alignment problems, there is no known polynomial algorithm
Even worse, most of these problems can be proven NP-complete, meaning that no such algorithm can exist!
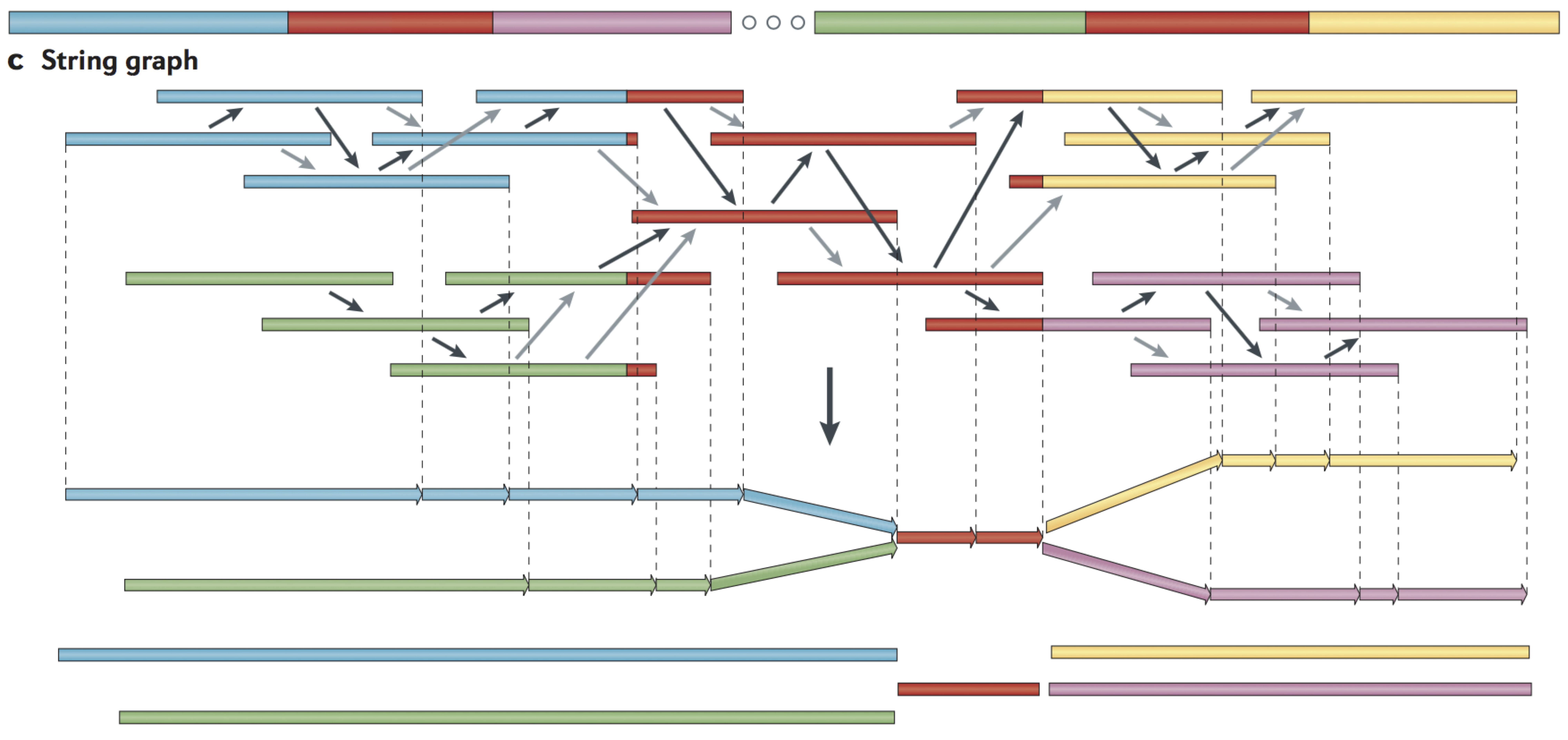
String graph
Alignments that may be transitively inferred from all pairwise alignments are removed
A graph is created with a vertex for the endpoint of every read
Edges are created both for each unaligned interval of a read and for each remaining pairwise overlap
Vertices connect edges that correspond to the reads that overlap
When there is allelic variation, alternative paths in the graph are formed
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4745987/
Real-world assembly methods
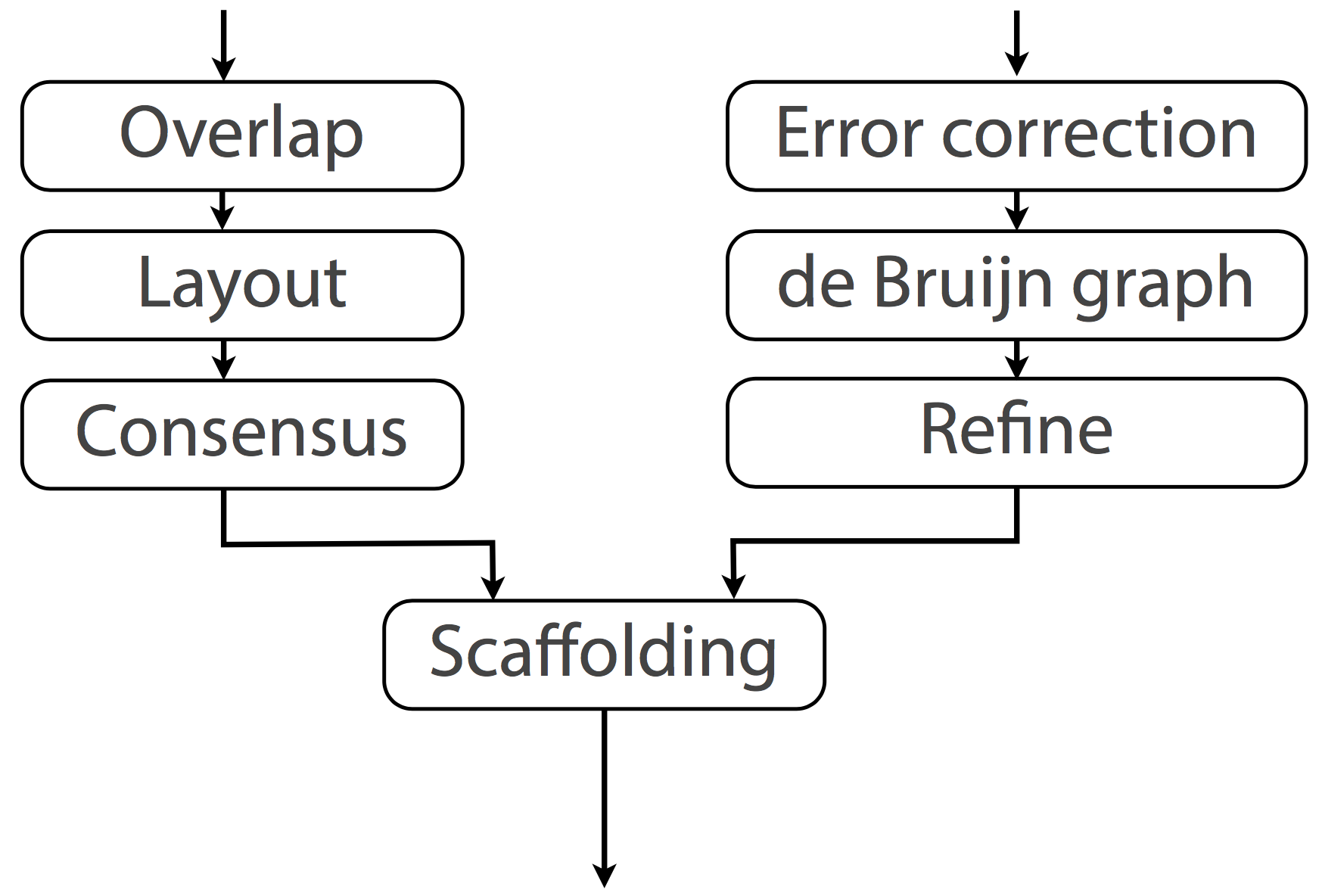
OLC - Overlap-Layout-Consensus assembly
DBG - De Bruijn graph assembly
Both handle unresolvable repeats by essentially leaving them out
Unresolvable repeats break the assembly into fragments Fragments are contigs (short for contiguous)
Overlap‐layout‐consensus (OLC)

Overlap graph formulation
Treat each sequence as a "node"
Draw an edge between two nodes if there is significant overlap between the two sequences
Hopefully the contig covers all or large number of sequences, once for each sequence
In other words, we are looking for Hamiltonian path in the overlap graph
Pros: straightforward formulation
Cons: no efficient accurate algorithm; repeats
Overlap‐layout‐consensus (OLC)
- All pairwise alignments (arrows) between reads (solid bars) are detected.
- Reads are merged into contigs (below the vertical arrow) until a read at a repeat boundary (split colour bar) is detected, leading to a repeat that is unresolved and collapsed into a single copy.
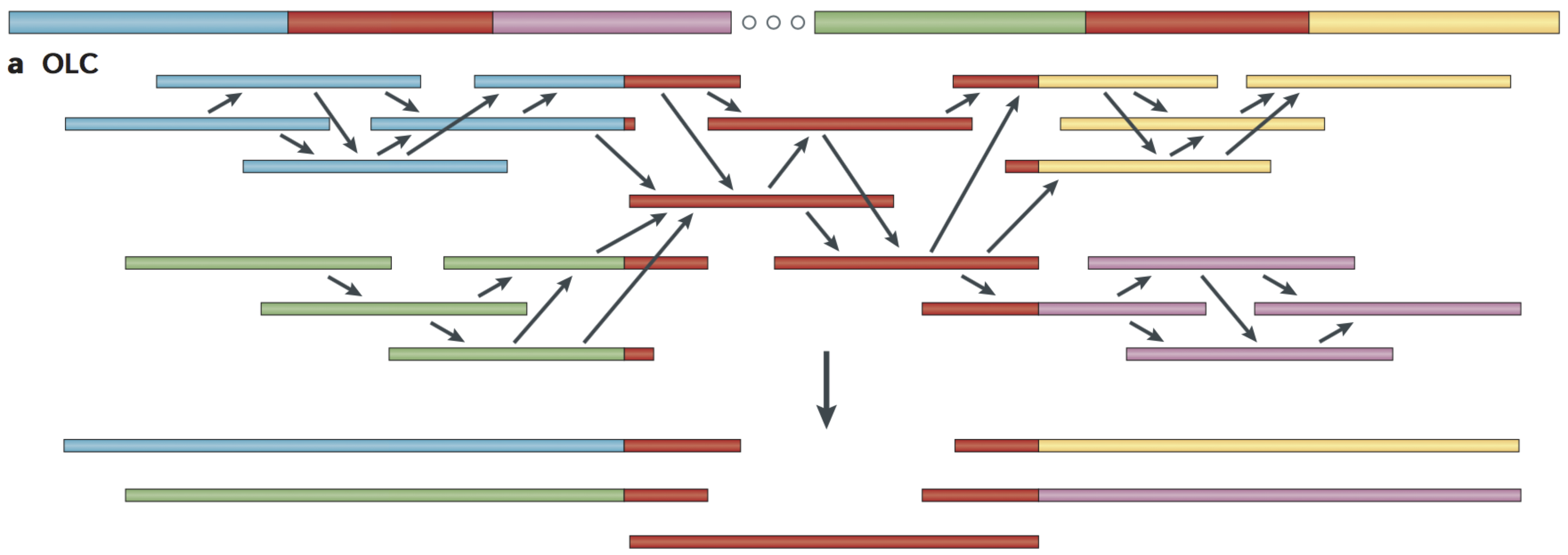
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4745987/
de Bruijn assembly
Reads are decomposed into overlapping k‐mers
Identical k‐mers are merged and connected by an edge when appearing adjacently in reads
Contigs are formed by merging chains of k‐mers until repeat boundaries are reached
If a k‐mer appears in multiple positions (red segment) in the genome, it will fragment assemblies and additional graph operations must be applied to resolve such small repeats
The k‐mer approach is ideal for short‐read data generated by massively parallel sequencing (MPS)
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4745987/
de Bruijn assembly
- An example of the decomposition for k = 3 nucleotides is shown, although in practice k ranges between 31 and 200 nucleotides
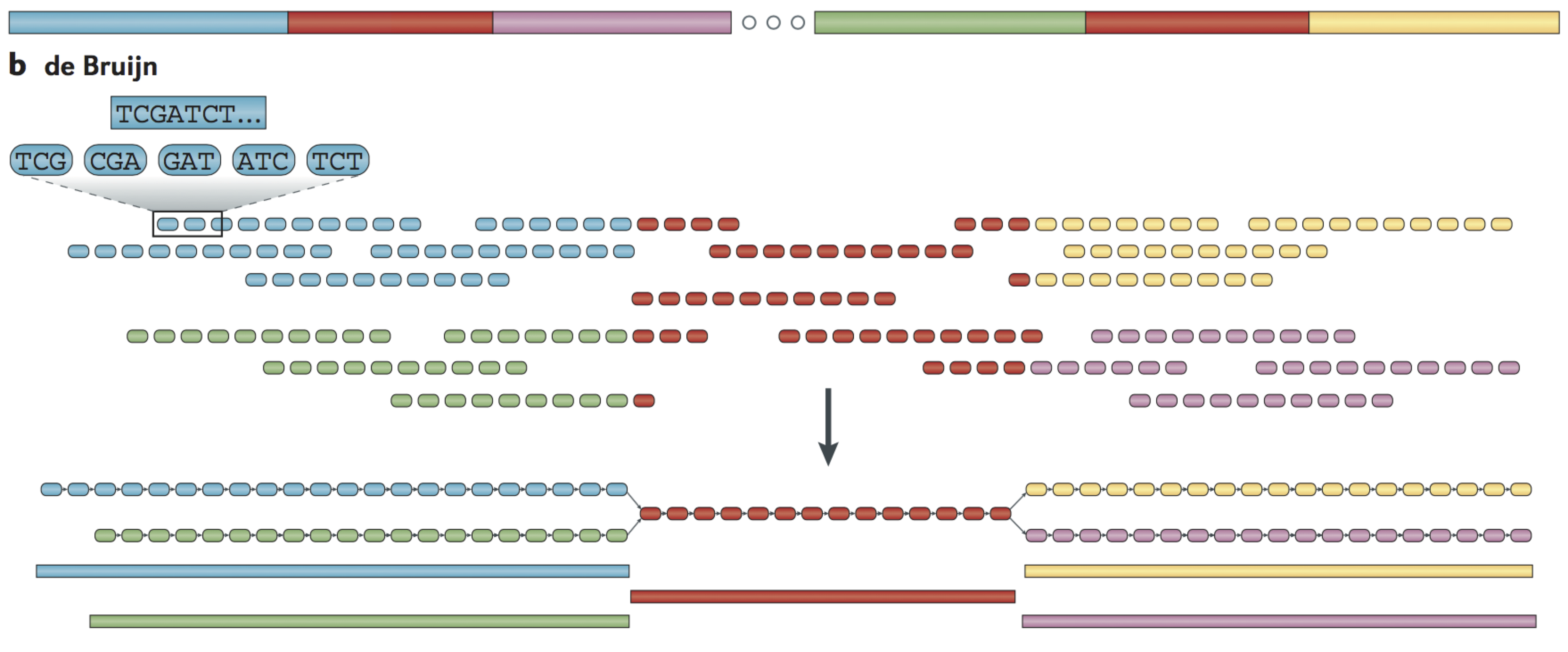
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4745987/
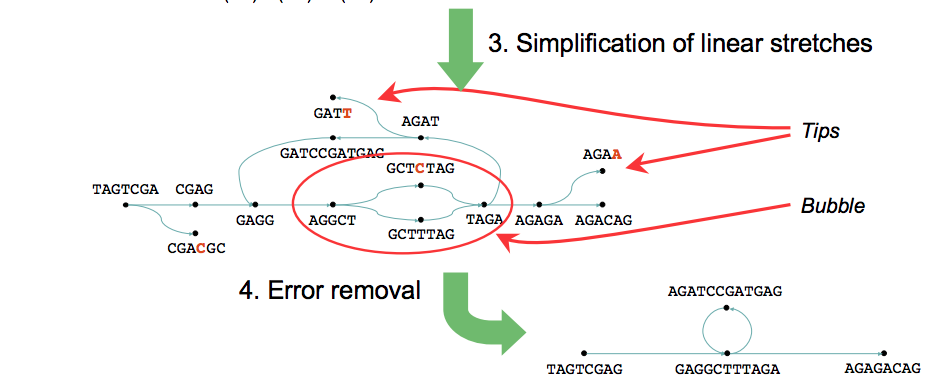
de Bruijn assembly problems
Erroneous data create three types of graph structures:
"tips" due to errors at the edges of reads
"bulges" due to internal read errors or to nearby tips connecting
erroneous connections due to cloning errors or to distant merging tips
Velvet: de novo assembly using very short reads
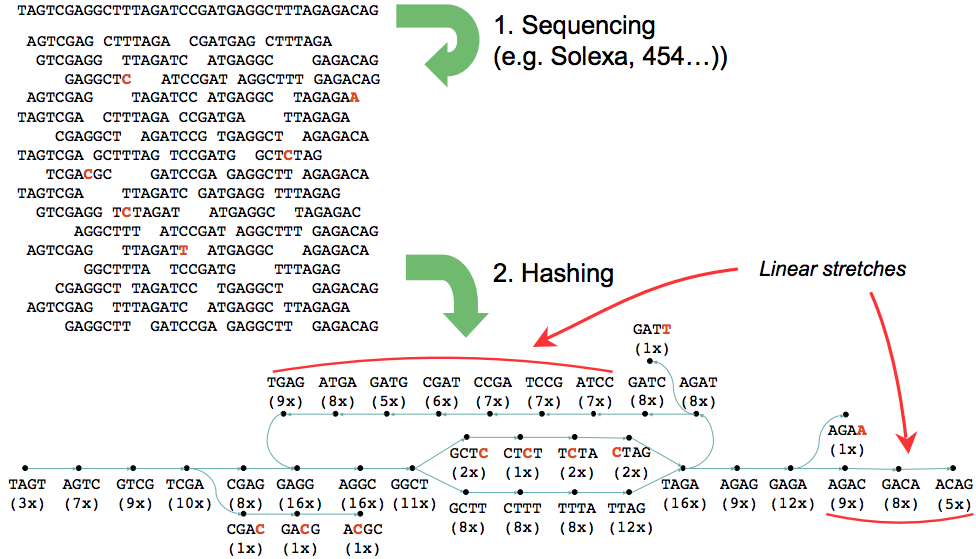
Velvet: de novo assembly using de Bruijn graph
https://www.ebi.ac.uk/~zerbino/velvet/
Zerbino, Daniel R., and Ewan Birney. "Velvet: Algorithms for de Novo Short Read Assembly Using de Bruijn Graphs." Genome Research, (May 2008)
Alignment problems
The genome being sequenced contains genomic variants
Reads contain two kinds of errors: base substitutions and indels. Base substitutions occur with a frequency from 0.5 – 2%. Indels occur roughly 10 times less frequently
Strand orientation is unknown
Computers excel at finding exact matches. Errors should be explicitly handled
"Fuzzy" pattern matching is much more computationally expensive
Alignment problems
> 50% of human genome is repeats - a major problem for fragment assembly
Over 1 million Alu repeats (about 300 bp)
About 200,000 LINE repeats (1000 bp and longer)

Alignment with repeats

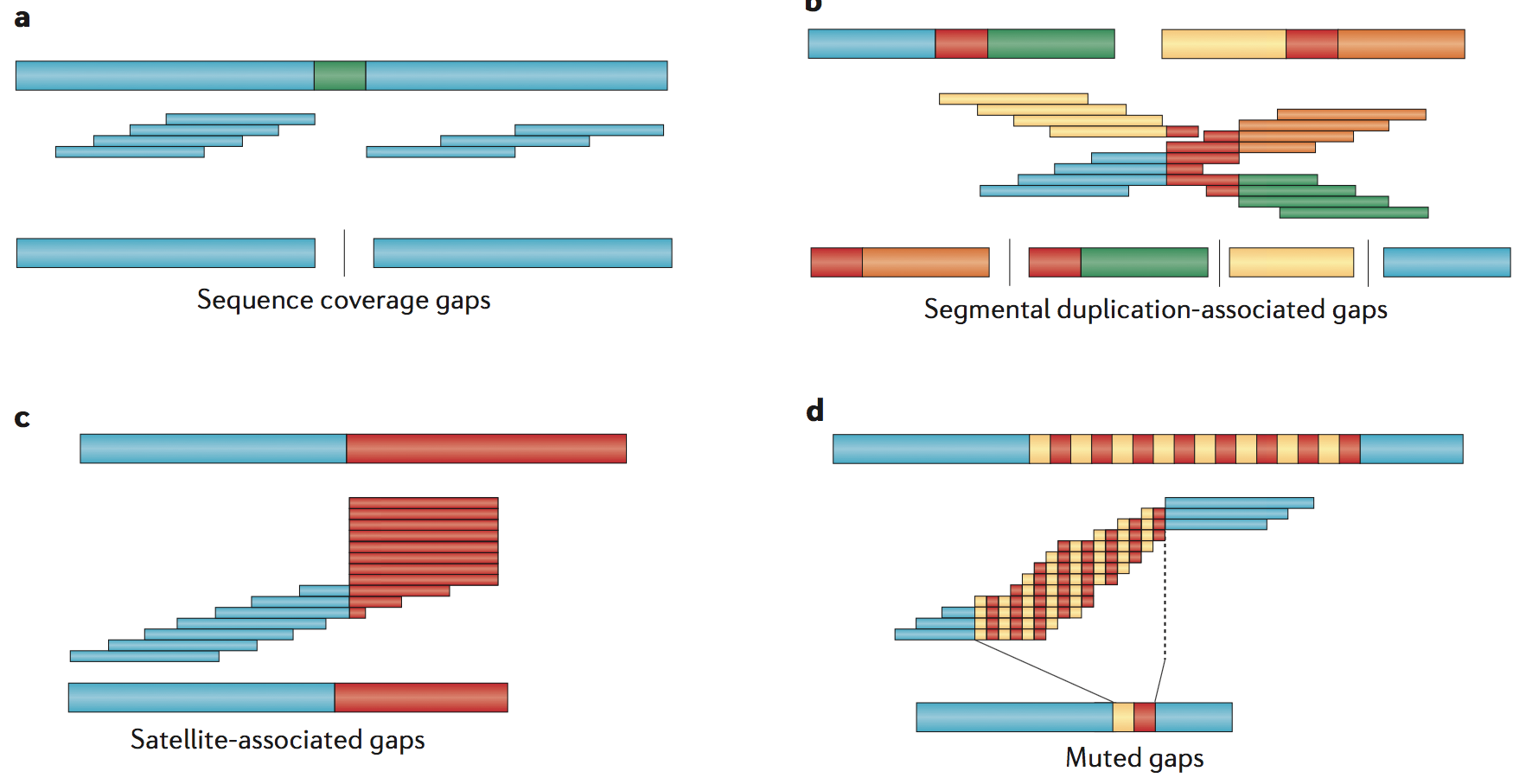
Gaps
Sequence-coverage gaps - Sequencing gaps occur, under the simplest condition, where no sequence reads have been sampled for a particular portion of the genome
Segmental duplication-associated gaps - Over one-third (206/540) of the euchromatic gaps in the human reference genome (GRCh38) are flanked by large, highly identical segmental duplications
Satellite-associated gaps - These include short and long runs of tandem repeats designated as short tandem repeats (STRs; also known as microsatellites), variable number of tandem repeats (VNTRs; also known as macrosatellites) and Mb-sized centromeric satellite repeats
Gaps
Muted gaps - Muted gaps are defined as regions that are inadvertently closed in an assembly but that actually show additional or different sequences in the vast majority of individuals
Allelic variation gaps - Some regions of a genome also show extraordinary patterns of allelic variation, often reflecting deep evolutionary coalescence
Coverage
The coverage of a sequencing project is the ratio of the total sequenced fragment length to the genome length, i.e. nl/T
Gaps are very difficult and expensive to close in any sequencing strategy, meaning that very high coverage is necessary to use shotgun sequencing on a large genome
Evaluating Assemblies
Coverage is a measure of how deeply a region has been sequenced
The Lander-Waterman model predicts 8-10 fold coverage is needed to minimze the number of contigs for a 1 Mbp genome
The N50 length is a statistics in genomics defined as the shortest contig at which half of the total length of the assembly is made of contigs of that length or greater
It is commonly used as a metric to summarize the contiguity of an assembly
Longer sequencing to complete human genomes
- Human genome is incomplete - ~160 gaps in euchromatin
- ~55% of them have been closed using Oxford Nanopore technology

https://www.nature.com/nature/journal/v517/n7536/full/nature13907.html
Improving the Human Reference Genome(s)

http://genome.wustl.edu/projects/detail/reference-genomes-improvement/
Jain, Miten, Sergey Koren, Karen H Miga, Josh Quick, Arthur C Rand, Thomas A Sasani, John R Tyson, et al. “Nanopore Sequencing and Assembly of a Human Genome with Ultra-Long Reads.” Nature Biotechnology, January 29, 2018. https://doi.org/10.1038/nbt.4060. - MinION nanopore sequencing to sequence human genome. Closed 12 gaps, fully typed MHC region. PCR-free sequencing preserves epigenetic modifications. Canu genome assembler. GraphMap, Minimap2 for mapping long reads. SVTyper, LUMPY for structural variants.
https://www.genengnews.com/gen-exclusives/first-nanopore-sequencing-of-human-genome/77901044
Longer reads - more errors
The increased read length and error rate of single-molecule sequencing has challenged genome assembly programs originally designed for shorter, highly accurate reads
Several new approaches have been developed to address this, roughly categorized as hybrid, hierarchical, or direct
Longer reads - more errors
Hybrid methods use single-molecule reads to reconstruct the long-range structure of the genome, but rely on complementary short reads for accurate base calls
Hierarchical methods do not require a secondary technology and instead use multiple rounds of read overlapping (alignment) and correction to improve the quality of the single-mol- ecule reads prior to assembly
Direct methods attempt to assemble single-molecule reads from a single overlapping step without any prior correction
Hierarchical strategy is the most suitable to produce continuous de novo assembly
Global and local alignment
Global alignment - comparing two sequences over their entire length, identifying long insertion and deletion. Identifying every mutation in your sequences
Local alignment - comparing sequences with partial homology. Making high-quality alignment